原标题:初中数学复习,整式运算的几何背景与应用,常考题型解析!
整式运算的几何背景+运用
01
整式运算的几何意义
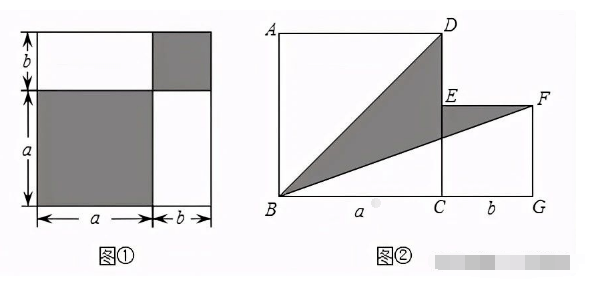
例题1:我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图1可以用来解释a2-b2=(a+b)(a-b).那么通过图2面积的计算,验证了一个恒等式,此等式是

分析:此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是大正方形的面积减去小正方形的面积,还可以表示成4个小长方形的面积。
解:由图②,可知:大正方形的面积为:(a+b)^2,小正方形的面积为(a-b)^2,
∴阴影部分的面积为:(a+b)^2-(a-b)^2,
部分阴影部分的面积还可表示为:4ab,
∴(a+b)^2-(a-b)^2=4ab.
这类题目解题的关键在于对图形的分割与拼合,会用多种方法表示同一图形的面积,然后抓住同一图形的面积相等,得到关系式。
02
公式法几何意义
例题2:请认真观察图形,解答下列问题:
(1)根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;
(2)在(1)的条件下,如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
解:(1)方法一:两个正方形的面积和,即a^2+b^2,
方法二:边长为a+b的正方形的面积减去两个空白的长方形的面积,即(a+b)^2-2ab,因此有a^2+b^2=(a+b)^2-2ab,
(2)图②阴影部分的面积是两个边长分别为a、b的正方形的面积和减去两个直角三角形的面积,即a^2+b^2-1/2a×a-1/2(a+b)×b=1/2a^2+1/2b^2-1/2ab=1、2(a^2+b^2-ab)=1/2[(a+b)^2-3ab],当a+b=ab=9时,原式=1/2×(81-27)=27,
答:阴影部分的面积为27.
本题考查完全平方公式的几何背景,用不同的方法表示同一个图形的面积是得出关系式的前提。当然,题目一般不会如此简单,会考查完全平方公式的变形,因此也需要掌握完全平方公式的各种变形公式。
03
因式分解几何背景
例题3:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到(a+2b)(a+b)=a^2+3ab+2b^2.
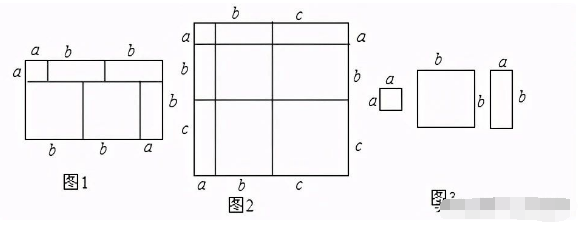
请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a^2+b^2+c^2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,请利用所给的纸片拼出一个长方形,使它的面积为2a^2+5ab+2b^2,把拼出的图形画在方框内,并拼出的图形将多项式2a^2+5ab+2b^2分解因式.
分析:(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.
(2)利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.
(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件.

中考数学常见9种出题形式,提前了解准没错!
初中数学必背定理、公式大全,初一初二预习,初三复习!
初中数学7-9年级,各类公式大全,必须要掌握!
中考数学答题技巧整理,掌握多拿20分!
初中数学考试避免这些低级错误,让你少丢20-30分!
初中数学7-9年级下册要点难点分析,考点全都这里!
声明:本文内容来源于网络,转载请联系原出处。中考君尊重版权,如有侵权问题,请及时与管理员联系处理。返回搜狐,查看更多
责任编辑:

