看全文,点击链接,加入wx公众号:楠喃书语
在图形与几何这一部分,《标准》将其划分为了两个部分,分别是图形的认识与测量、图形的位置与运动。
图形的认识,实则是在建立起点、线、面、体之间的结构关系,需要类比迁移来进行学习。
图形的测量则是对于图形的再认识,是对于图形特征的模式应用,需要建立长度、角度、周长、面积、体积之间的关系,这些也可属于同一类度量知识,学习的轨迹极为相似,皆需要感受度量单位的意义(1厘米有多长?),经历统一单位长度的过程(为什么要统一“厘米”这个单位?)。
要测量图形,就必须认识图形,对于某一个图形的认识的核心要素便是对于图形的特征描述,譬如:测量长方形的周长,那么学生首先就必须认识到长方形的两对边是相等的关系。
而图形的认识需要图形的测量进行验证,譬如:要知道三角形的内角和是180度,那么学生可以剪下三个角,同时放在一个水平线上,然后用量角尺进行度量,从而得出结论。
图形运动的本质是图形中各点的位置变化。描述图形位置的变化需要通过平面内精确的有序数对来阐释,也体现了数形结合在此的功能与用途。若要区别图形位置变化的特点,便要理解图形运动的基本轨迹——平移、旋转和翻转(轴对称),此时,图形的运动中所体现出来的变与不变,更有利于学生感受到数学的和谐堆成美
从例题中,我总结了图形与几何部分的几大关键要素:
发现周长、面积、体积知识之间的结构关系——由体到面、由面到线例24找出对应图形中,让学生从立体图形中描出平面图形的过程,有利于学生建立面积和体积之间的关系,更系统地理解面的形成过程。
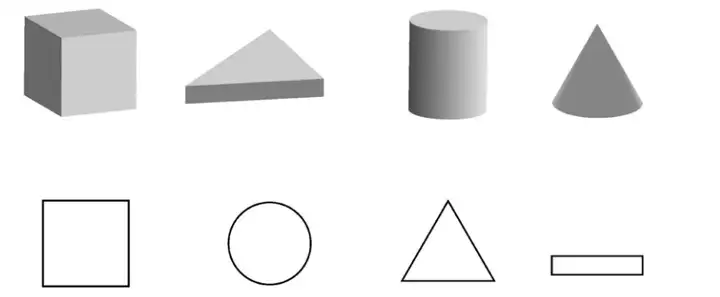
同时,从立体图形中抽象剥离出平面图形,及时地建立了立体图形和平面图形两者之间的紧密关系。也将儿童的几何思维,从有棱有角的三维空间,转向了平整光滑的二维视角,更能帮助学生感受到平面图形“面”的特征,符合儿童几何思维的抽象层次。设计中,引导学生盖印操作的过程,也充分展现了课堂中由体至面、体面结合的概念渗透。
此例题也为后期从“面”中抽象出“一维线段”埋下了相似的学习轨迹,其教学路径皆遵循从部分回归整体的理念,如例29所示。
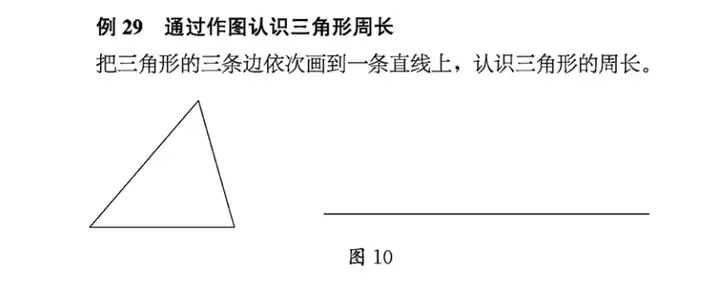
很多老师会感受到,学生在五年级时,总是会混淆周长和面积的公式。为何?实质上是因为对于何是周长、何是面积缺乏量的感受,换句话来说,是对于何为线段、何为面积缺乏直观的感受。如果学生亲自触摸感受过线与面的形成、累加过程,才能积累与此相关的量感。
此例题给予我们的课堂一定的启示,线与面是万万不可分割开来学习的。学周长,不是让孩子们背诵“封闭图形一周的长度”,而是要让概念模型立体化,让孩子们感受在面的周围“包边”的过程。
我曾看过一个教学案例,老师的教学设计很独特:为了避免小狼的追击,请同学们为可爱小羊的住所围一个栅栏,有圆形的、长方形的、爱心形的。孩子们在故事的情境中,学生意识到包边的过程一定要首尾相连、不留缝隙,不然小狼会从缝隙中溜进去。从头到尾,教师没说一句话,只是静静地看着孩子们做出包、围、贴等操作,却不费吹灰之力地渗透了周长线段的量感,多么神奇地一件事!
二、在推测和估测中培养量感的直觉性
(《课标》中例25,以长度单位的四题为例,来具体讲述量感的培养策略。“量感”是此次新课标中增添的一大主要内容,其重要性可与十大核心素养之一——“数感”相提并论。“量感”是指学生在具体的实际情境中能够主动、自觉性地理解和运用“量”的态度和意识。

量感,是一种直觉和感官意识,更是对事物长短、轻重、大小等量的感性认识,而此感性认识是建立于学生对于单位长度的意义理解之上的,而非仅仅是凭借自己的感觉。
对于量感的培养分为两点:第一,是对于量的区分,即在具体情境中,辨别和区分某一量,譬如:区分1cm、1dm、1m、1km等长度单位的具体长短;第二,是对于量的推断。能够在不借助测量工具的前提之下,推测出物体的具体长度或者能为物体选择合适的长度单位。
“量的推断”离不开对于“量的区分”,例如:要推理判断黑板大概有多长?那么学生首先要选择一个合适的参照物,此参照物便是一个测量的“度”,如果学生选择用1米的长度作为参照,就必须在选择之前,理解1米的具体长度意义。
例33:估测不规则图形的面积

“面积”一课,从历史的角度来说,其源自于尼罗河的泛滥,尼罗河成就了古埃及的文明,却也给古埃及人的农业带来了一定的烦恼。每年7月份,尼罗河水泛滥,水位海拔升高,便摧毁了庄稼和农田,也抹去了各庄稼之间的界限,等到水位下降之后,又要重新划界限,久而久之就有了“面积”一说。
但面积的大小如何进行计算呢?如上图所示,这张图的巧妙点在于,他不是一个规则图形,学生可能已经通过数格子、移动格子、拼接格子等过程,得到了各种各样的数据200、250、270,但到底是多少呢?
学生会慢慢地发现,实则在一个范围中,围绕边线最小的矩形中包含了272个小正方形(蓝色区域),而曲线内部完整的小正方形却只有161个(绿色区域)。
那么这道题的目的便不在于求得一个精确值,而在于一个有上界和下界的范围值。这个问题正是在累积“面积单位”的过程,用1平方厘米的小正方形进行密铺,便能知道其面积大小,学生在数格子的过程中建立了对于面积的量感,也更好的感受到了小单位累积性的特征以及面积的概念意义。

