今天,给大家整理了小学数学思维训练题,赶快来练习一下吧~
一年级
1、把下面的图形剪成四等份,要求剪成的每个小图形形状、大小都一样,怎么剪?
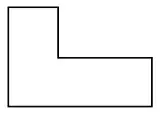
【答案】

2、六一节时,同学们互相送卡片,如果每人接到卡片后,要回送一张卡片.问所送卡片的总数是单数还是双数?
【解析】
双数
3、从0,2,4,6,8这五张数字卡片中,每次抽出两张组成一个两位数.组成的两位数中,最大的是( ),最小的是( ).组成不同的三位数,最大的是:( ),最小的是( ).
【解析】
从0,2,4,6,8这五张数字卡片中,每次抽出两张组成一个两位数.可以组成的数中,十位最大是8,剩下的数中个位最大是6,所以最大的数是86;
十位最小是2,剩下的数中个位最小是0,所以最小的数是20。
组成不同的三位数,百位最大是8,剩下的数中十位最大是6,再剩下的数中个位最大是4,最大的是864;
百位最小是2,剩下的数中十位最小是0,再剩下的数中个位最小是4,最小的是204。
【答案】
86;20;864;204
二年级
1、小明、小佳、小马一共有27张积分卡,小明比小佳多2张,小佳比小马多2张,问他们三人各有几张积分卡?
【解答】
小明11张,小佳9张,小马7张
2、小明用10元钱买5角邮票和2角邮票,共买了23张,两种邮票各有多少张?
【解答】
假设这23张邮票全部都是2角的,则:2×23=4元6角;10-4元6角=5元4角;5元4角÷(5角-2角)=18(张);23-18=5(张)所以,买了18张5角的邮票,5张2角的邮票。
3、一筐葡萄,连筐共重68千克,先卖出葡萄的一半,再卖出剩下的一半,这时连筐还重20千克,原来这筐葡萄重多少千克?
【解答】
68-20=48(千克);48÷3=16(千克);16×4=64(千克)
三年级
1、3只猫3天吃了3只老鼠,照这样的效率,9只猫9天能吃( )只。
【解析】
事情发生的同时性,3只猫3天吃了3只老鼠,说明3只猫1天吃了1只老鼠,所以9只猫9天能吃27只。
2、┖┴┴┴┴┴┴┴┴┴┚图中共有( )条线段。
【解析】
几何计数,数线段,直接利用公式,这条线段分成了10份,所以图中线段的总条数为:1+2+3+4+5+6+7+8+9+10=55条
3、一个正方形,被分成5个相等的长方形,每个长方形的周长是60厘米,正方形的周长是多少厘米
【解析】
长方形的短边长为正方形的边长的1/5,长边长为正方形的边长。
所以长方形的短边长:长边长=1:5;
60÷【(1+5)×2】=5(厘米)
则长方形的短边长为5厘米,
长边长为25厘米。
所以正方形的边长为25厘米,即正方形的周长为25×4=100厘米。
四年级
1、计算:2+5+8+…+23+26+29
【解答】
这是一个公差为3、首项为2、末项为29、项数为(29-2)÷3+1=10的等差数列求和,
原式=(2+29)×10÷2=31×10÷2=155.
2、计算:(2+4+6+…+100)-(1+3+5+…十99)
【解析】
解法一
原式=(2+100)×50÷2-(1+99)×50÷2
=2550-2500=50,
解法二
原式=(2-1)+(4-3)+(6-5)+…+(100-99)
=1×50=50.
3、计算:
1÷2010+2÷2010+3÷2010+…+2008÷2010+2009÷2010+2010÷2010
【解答】
如果按照原式的顺序,先算各个商,再求和,既繁又难,由于除数都相同,被除数组成一个等差数列:
1,2,3,4,…,2008,2009,2010.
所以可根据除法的运算性质,先求全部被除数的和,再求商
解原式=(1+2+3+…+2009+2010)÷2010
=(1+2010)×2010÷2÷2010
=1005.5
五年级
1、甲、乙两地相距420千米,一辆汽车从甲地开到乙地共用了8小时,途中,有一段路在整修路面,汽车行驶这段路时每小时只能行20千米,其余时间每小时行60千米。整修路面的一段路长多少千米?
【解析】
假如这8小时都是每小时行60千米,就比实际行的路程多出了60×8-420=60千米。在8小时里,只要有1小时行驶在整修路面的公路上,汽车就少行60-20=40千米,60里面有1.5个40,因此,汽车在整修路面的公路上行驶了1.5小时,路长20×1.5=30千米。
2、客、货两车同时从甲、乙两站相对开出,客车每小时行54千米,货车每小时行48千米。两车相遇后又以原速前进,到达对方站后立即返回,两车再次相遇时客车比货车多行21.6千米。甲、乙两站间的路程是多少千米?
【解析】
客货两车从出发到第二次相遇,一共行了三个全程。而第二次相遇时客车比货车多行了21.6千米,说明两车已行了21.6÷(54-48)=3.6小时。用速度和乘所行时间就得到三个路程的和,再除以3就得到甲、乙两站间的路程。
3、两地相距460千米,甲列车开出2小时后,乙列车与甲列车相向开出,经过4小时与甲列车相遇。已知甲列车每小时比乙列车多行10千米,求甲列车每小时行多少千米?
【解析】
甲列车4小时比乙列车4小时多行10×4=40千米。因此,甲列车先行2小时,又行4小时,如果再行4小时就一共能行460+40=500千米。所以,甲列车的速度是每小时行500÷(2+4×2)=50千米。
六年级
1、求1992×59除以7的余数。
【解析】
可将1992×59转化为求1992除以7和59除以7的余数的乘积,使计算简化。1992除以7余4,59除以7余3。根据同余性质,“4×3”除以7的余数与“1992×59”除以7的余数应该是相同的,通过求“4×3”除以7的余数就可知道1992×59除以7的余数了。因为1992×59≡4×3≡5(mod7)所以1992×59除以7的余数是5。
2、已知2001年的国庆节是星期一,求2010年的国庆节是星期几?
【解析】
一星期有7天,要求2010年的国庆节是星期几,就要求从2001年到2010年的国庆节的总天数被7除的余数就行了。但在甲酸中,如果我们能充分利用同余性质,就可以不必算出这个总天数。2001年国庆节到2010年国庆节之间共有2个闰年7个平年,即有“366×2+365×7”天。因为366×2≡2×2≡4(mod7),365×7≡1×7≡0(mod7),366×2+365×7≡2×2+1×7≡4+0≡4(mod7)答:2010年的国庆节是星期五。

